Back when I first read the RL textbook, the Bellman Equation for the discounted value function was introduced as:

Now, I felt there was a big jump from the third equation to the fourth, so recently I came back to it. Turns out, the derivation from that third equation the the fourth was quite significant! So let’s break it down:

\[\begin{aligned} v_{\pi}(s) &= \mathbb{E}[G_t | S_t = s]\\ &= \mathbb{E}[R_{t+1} + \gamma G_{t+1}| S_t = s]\\ &= \mathbb{E}[R_{t+1}|S_t=s] + \gamma \mathbb{E}[G_{t+1}| S_t = s] \qquad (1) \end{aligned}\]

Before we expand these two terms, let us revisit some basic probability.

\[\begin{aligned} \mathbb{E}[A] = \mathbb{E}\big[\mathbb{E}[A|B]\big] \end{aligned}\]

Why is this true? Let’s expand the RHS.

\[\begin{aligned} \mathbb{E}\big[\mathbb{E}[A|B]\big] &= \sum_{b\in\mathcal{B}} p(B=b)\;\mathbb{E}[A|B=b] \\ &= \sum_{b\in\mathcal{B}} p(B=b) \sum_{a\in\mathcal{A}}a\;p(A=a|B=b)\\ &= \sum_{b\in\mathcal{B}} \sum_{a\in\mathcal{A}}a\;p(B=b)\;p(A=a|B=b)\\ &= \sum_{b\in\mathcal{B}} \sum_{a\in\mathcal{A}}a\;p(A=a,B=b)\\ &= \sum_{a\in\mathcal{A}}a\;\sum_{b\in\mathcal{B}}p(A=a,B=b)\\ &= \sum_{a\in\mathcal{A}}a\;p(A=a)\\ &=\mathbb{E}[A] \end{aligned}\]

What we did here is condition over another random variable and marginalize over it. Keeping this in mind, let us go back to the first term on the RHS in equation 1.

\[\begin{aligned} \mathbb{E}[R_{t+1}|S_t=s] &= \mathbb{E}\big[\mathbb{E}[R_{t+1}|S_t=s,A_t]\big]\\ &= \sum_{a}p(A_t=a|S_t=s)\;\mathbb{E}[R_{t+1}|S_t=s,A_t=a]\\ &= \sum_{a}\pi(a|s)\;\mathbb{E}[R_{t+1}|S_t=s,A_t=a]\\ &= \sum_{a}\pi(a|s)\;\mathbb{E}\big[\mathbb{E}[R_{t+1}|S_t=s,A_t=a,S_{t+1}]\big]\\ &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\mathbb{E}[R_{t+1}|S_t=s,A_t=a,S_{t+1}=s']\\ &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\;r(s,a,s') \qquad (2) \end{aligned}\]

Here, \(r(s,a,s')\) is the expected reward when action \(a\) is state \(s\) leads to state \(s'\).

Next, the second term (without \(\gamma\)) in the RHS of equation 1 can be similarly expanded as:

\[\begin{aligned} \mathbb{E}[G_{t+1}| S_t = s] &= \mathbb{E}\big[\mathbb{E}[G_{t+1}| S_t = s, S_{t+1}]\big] \\ &= \sum_{s'} \mathbb{E}[G_{t+1}| S_t = s, S_{t+1}=s']\; p(s'|s) \\ &= \sum_{s'} \mathbb{E}[G_{t+1}| S_t = s, S_{t+1}=s'] \sum_a p(a|s)\;p(s'|s,a)\\ &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \mathbb{E}[G_{t+1}| S_t = s, S_{t+1}=s']\\ &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \mathbb{E}[G_{t+1}| S_{t+1}=s'] \qquad (3) \end{aligned}\]

Substituting equations 2 and 3 back in 1, we get:

\[\begin{aligned} v_{\pi}(s) &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\;r(s,a,s') \\ &\quad + \gamma \sum_a \pi(a|s) \sum_{s'} p(s'|s,a)\;\mathbb{E}[G_{t+1}| S_t = s, S_{t+1}=s']\\ &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \big[r(s,a,s') + \gamma \mathbb{E}[G_{t+1}| S_t = s, S_{t+1}=s']\big]\\ &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \big[r(s,a,s') + \gamma \mathbb{E}[G_{t+1}|S_{t+1}=s']\big]\\ v_{\pi}(s) &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \big[r(s,a,s') + \gamma v_\pi(s')\big] \qquad (4) \end{aligned}\]

Tadaa!

Wait, you say, the Bellman equation in the book looks different from this…

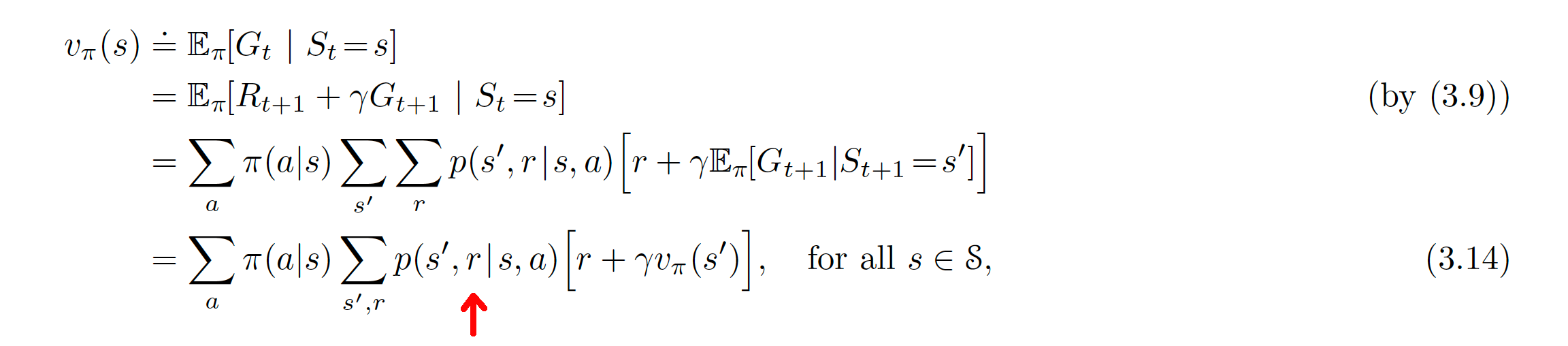
Hmm, let us look at the first term again:

\[\begin{aligned} \text{First term} &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\;r(s,a,s')\\ &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\;\mathbb{E}[R_{t+1}|S_t=s,A_t=a,S_{t+1}=s']\\ &= \sum_{a}\pi(a|s)\;\sum_{s'}p(s'|s,a)\sum_{r}p(r|s,a,s')\,r\\ &= \sum_{a}\pi(a|s)\;\sum_{s'}\sum_{r}p(s'|s,a)p(r|s,a,s')\,r\\ &= \sum_{a}\pi(a|s)\;\sum_{s',r}p(s',r|s,a)\,r \qquad (5) \end{aligned}\]

Starting to look more familiar, eh?

What happened in the last step there, you ask. Well, we applied the chain rule of conditional probability:

\[\begin{aligned} P(A|B,C,D)P(B|C,D) &= \dfrac{P(A,B,C,D)}{P(B,C,D)} \dfrac{P(B,C,D)}{P(C,D)} \\ &= \dfrac{P(A,B,C,D)}{P(C,D)} \\ &= P(A,B|C,D) \end{aligned}\]

We can also re-write the second term. There is no reward term here, and so:

\[\begin{aligned} \mathbb{E}[G_{t+1}| S_t = s] &= \sum_a \pi(a|s) \sum_{s'} p(s'|s,a) \;\mathbb{E}[G_{t+1}| S_{t+1}=s']\\ &= \sum_a \pi(a|s) \sum_{s'} \sum_r p(s',r|s,a)\;\mathbb{E}[G_{t+1}| S_{t+1}=s'] \\ &= \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a)\;\mathbb{E}[G_{t+1}| S_{t+1}=s'] \qquad(6)\\ \end{aligned}\]

Finally, substituting equations 5 and 6 back in 1:

\[\begin{aligned} v_{\pi}(s) &= \sum_{a}\pi(a|s)\;\sum_{s',r}p(s',r|s,a)\;r \\ &\quad + \gamma \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a)\;\mathbb{E}[G_{t+1}|S_{t+1}=s']\\ &= \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) \big[r + \gamma \mathbb{E}[G_{t+1}|S_{t+1}=s']\big]\\ v_{\pi}(s) &= \sum_a \pi(a|s) \sum_{s',r} p(s',r|s,a) \big[r + \gamma v_\pi(s')\big] \qquad (7) \end{aligned}\]

Ladies and gentlemen, the Bellman equation.

It was more nuanced that I expected.